Plot the relation between assumed parameters and requirements for achieving a target power (or other objective)

Plot (a slice of) an object of class power_array. Main purpose is to illustrate the relation between two parameters (e.g., effect size on the x-axis and n on the y-axis) for a given target power. An example may be highlighted by drawing an arrow at the combination of parameters deemed most likely.

Usage

PowerPlot(
  x,
  slicer = NULL,
  par_to_search = "n",
  example = NULL,
  find_lowest = TRUE,
  target_value = 0.9,
  target_at_least = TRUE,
  method = "step",
  summary_function = mean,
  target_levels = c(0.8, 0.9, 0.95),
  col = grDevices::grey.colors(1, 0.2, 0.2),
  shades_of_grey = TRUE,
  example_text = TRUE,
  title = NULL,
  par_labels = NULL,
  smooth = NA,
  ...
)

Arguments

x: An object of class power_array (from powergrid).
slicer: If the parameter grid for which `x' was constructed has more than 2 dimensions, a 2-dimensional slice may be cut out using slicer, which is a list whose elements define at which values (the list element value) of which parameter (the list element name) the slice should be cut out.
par_to_search: The variable whose minimum (or maximum, when find_lowest == FALSE) is searched for achieving the target_levels.
example: If not NULL, a list of length one, defining at which value (list element value) of which parameter (list element name) the example is drawn for a power of target_value. You may supply a vector longer than 1 for multiple examples.
find_lowest: Logical, indicating whether the example should be found that minimizes an assumption (e.g., minimal required n) to achieve the target_value or an example that maximizes this assumption (e.g., maximally allowed SD).
target_value: The power (or whatever the target is) for which the example, if requested, is drawn. Also defines which of the power lines is drawn with a thicker line width, among or in addition to the power lines defined by target_levels.
target_at_least: Logical. Should the target value be minimally achieved (e.g., power), or maximially allowed (e.g., estimation uncertainty).
method: Method used for finding the required par_to_search needed to achieve target_value. Either step: walking in steps along par_to_search or lm: Interpolating assuming a linear relation between par_to_search and (qnorm(x) + qnorm(1 - 0.05)) ^ 2. The setting lm is inspired on the implementation in the sse package by Thomas Fabbro.
summary_function: If x is an object of class power_array where attribute summarized is FALSE (and individual iterations are stored in dimension iter, the iterations dimension is aggregated by summary_fun. Otherwise ignored.
target_levels: For which levels of power (or whichever variable is contained in x) lines are drawn.
col: Color for the contour lines. Does not effect eventual example arrows. Therefore, use AddExample.
shades_of_grey: Logical indicating whether greylevels are painted in addition to isolines to show power levels.
example_text: When an example is drawn, should the the required par value be printed alongside the arrow(s)
title: Character string, if not NULL, replaces default figure title.
par_labels: Named vector with elements named as the parameters plotted, with as values the desired labels.
smooth: Numeric, defaults to NA, meaning no smoothing. Non NA value is used as argument span for smoothing with stats::loess, regressing the contour values on the x and y-axis. Suggested value is .35. Functionality implemented for consistency with sse package, but use is discouraged, since regressing the contour values flattens the contour plot, thereby biasing the contour lines.
...: Further arguments are passed on to function image internally. Most useful for zooming with xlim and ylim.

Value

A list containing the coordinate arguments x, y, and z, as passed to image() internally.

Details

The most common use case may be plotting the required n (on the y-axis) as a function of some other parameter (e.g., effect size, on the x-axis) for achieving a certain level of statistical power. The default argument settings reflect this use case.

Flexible plotting

The plotting is, however, more flexible.

Any variable on the axes

You can flip the axes by setting a different par_to_search (which defines the y-axis). The other parameter is automatically chosen to be drawn on the x-axis.

Maximizing a parameter

One may also search not the minimum, as in the case of sample size, but the maximum, e.g., the highest sd at which a certain power may still be achieved. In this case, the par_to_search is sd, and find_lowest = FALSE.

When smaller is better

In the standard case of power, higher is better, so you search for a minimal level of power. One may however also aim at, e.g., a maximal width of a confidence interval. For this purpose, set target_at_least to FALSE. See Example for more details about find_lowest and target_at_least.

Author

Gilles Dutilh

Examples

## ============================================
## Typical use case: minimal n for power
## ============================================
## What's the minimal sample size n, given the combination of sd and delta.

## Set up a grid of n, delta and sd:
sse_pars = list(
  n = seq(from = 10, to = 60, by = 4),
  delta = seq(from = 0.5, to = 1.5, by = 0.1), # effect size
  sd = seq(.1, 1.1, .2)) # Standard deviation

## Define a power function using these parameters:
PowFun <- function(n, delta, sd){ # power for a t-test at alpha = .05
  ptt = power.t.test(n = n/2, delta = delta, sd = sd,
                     sig.level = 0.05)
  return(ptt$power)
}

## Evaluate PowFun across the grid defined by sse_pars:
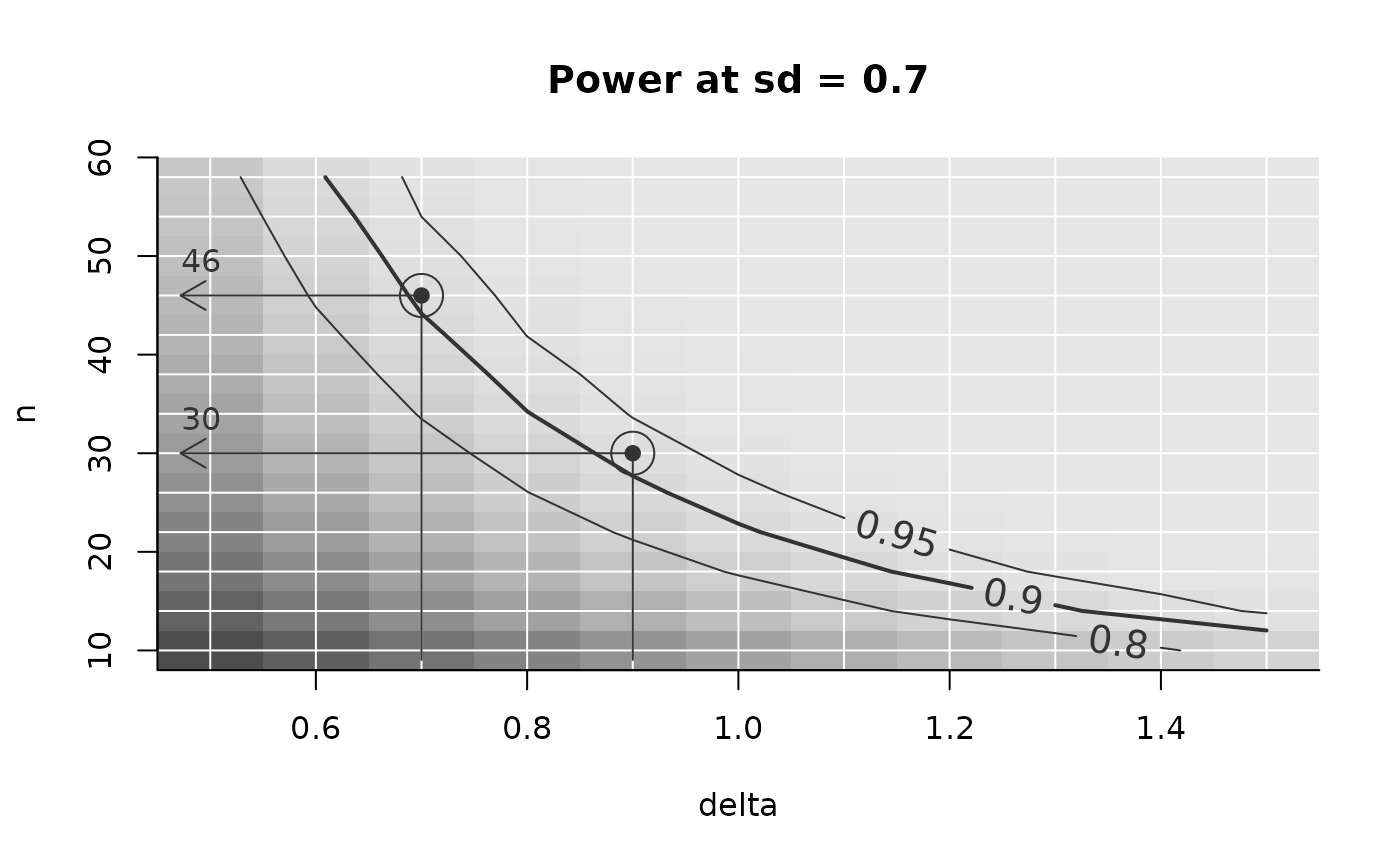
power_array = PowerGrid(pars = sse_pars, fun = PowFun, n_iter = NA)

## explore power graphically in the situation where sd = .7, including an
## example situation where delta is .9:
PowerPlot(power_array,
          slicer = list(sd = .7),
          example = list(delta = c(.7, .9)), # two examples
          target_value = .9 # 90% power
          )


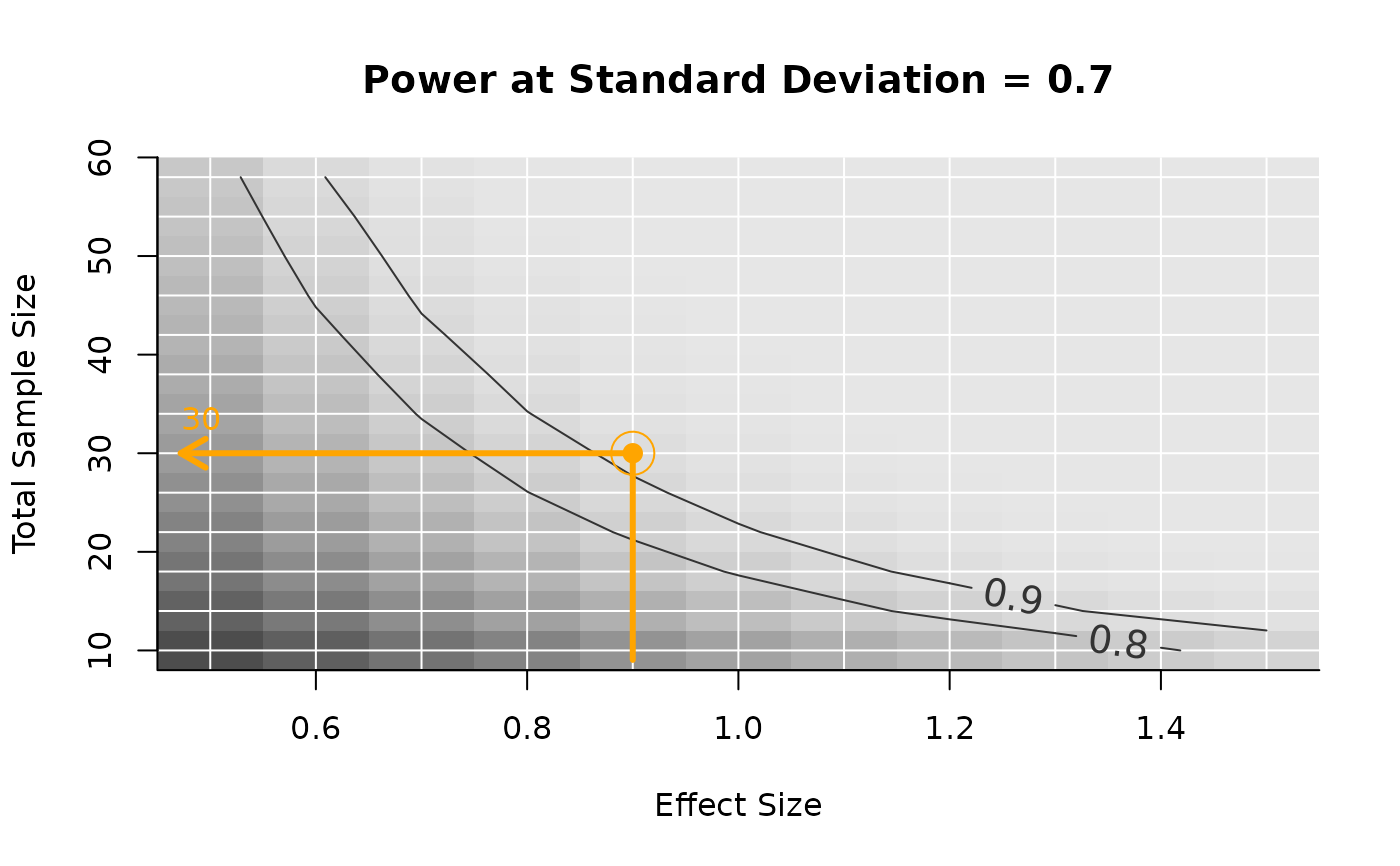
## Some graphical adjustments. Note that example is drawn on top of
## PowerPlot now.
PowerPlot(power_array,
          slicer = list(sd = .7),
          par_labels = c(n = 'Total Sample Size',
                         delta = 'Effect Size',
                         sd = 'Standard Deviation'),
          target_levels = c(.8, .9), # draw fewer power isolines
          target_value = NA # no specific power target (no line thicker)
          )
AddExample(power_array,
           slicer = list(sd = .7),
           example = list(delta = .9),
           target_value = .9,
           col = 'Orange', lwd = 3)


## ============================================
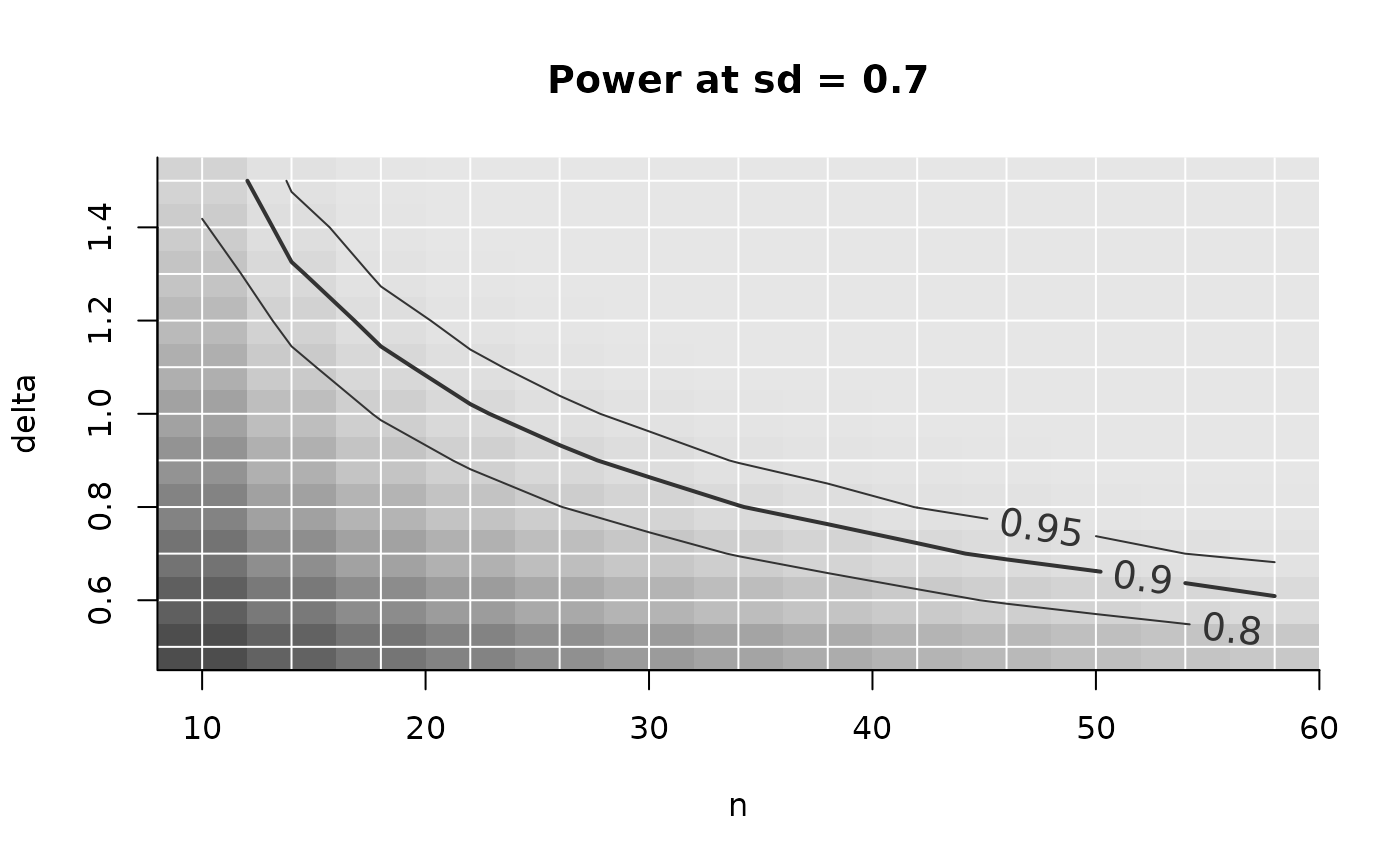
## Less typical use case:
## minimal delta for power, given sd, as a function of n
## ============================================
## You can easily change what you search for. For example: At each sample size n,
## what would be the minimal effect size delta there must be for the target
## power to be achieved?

PowerPlot(power_array,
          par_to_search = 'delta',
          slicer = list(sd = .7))


## ============================================
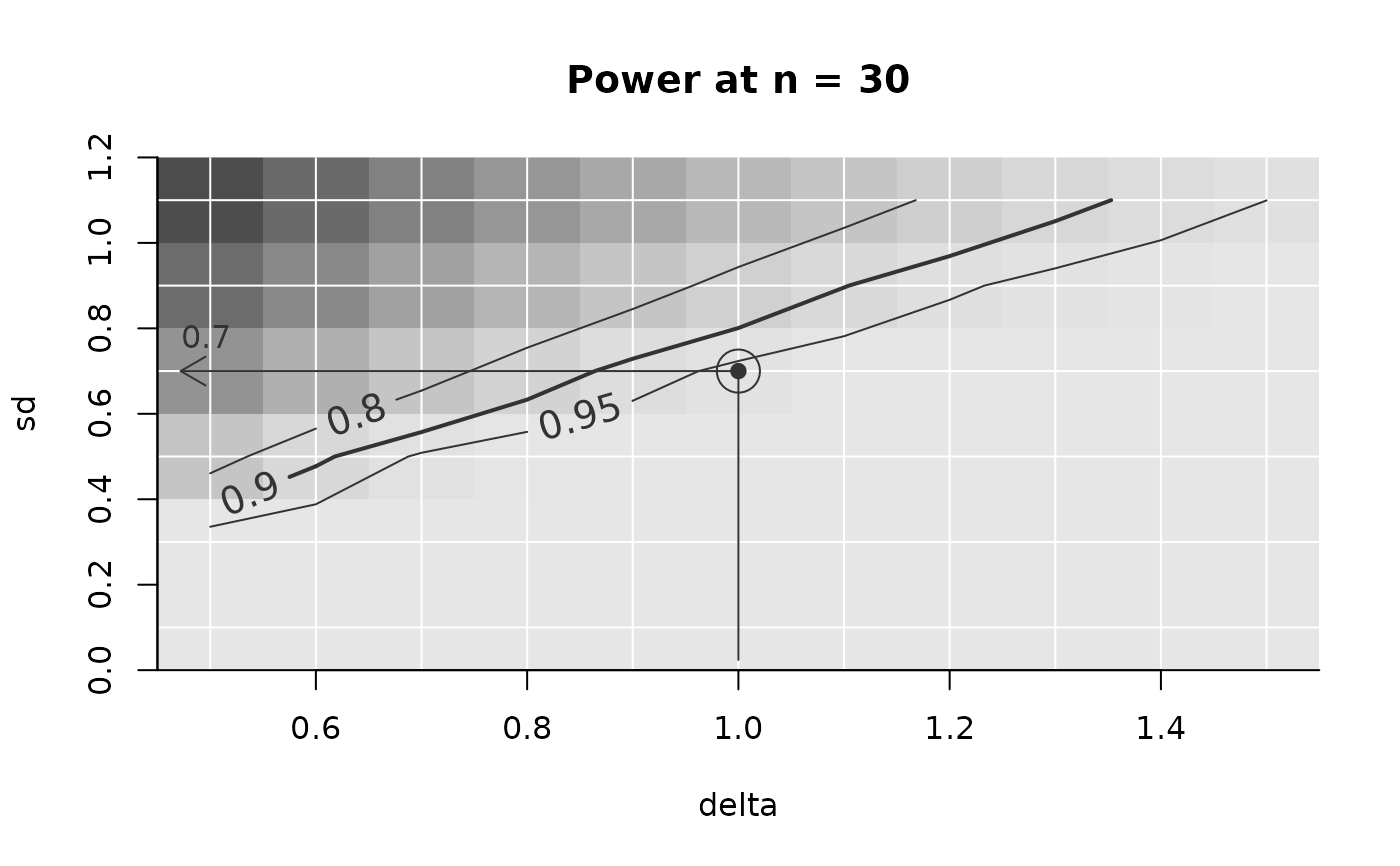
## Less typical use case:
## *maximum sd* for power, given n, as a function of delta
## ============================================
## You're not limited to study n at all, nor to searching a minimum: When
## your n is given to be 30, what is the largest sd at which we still find
## enough power? (as a function of delta on the x-axis)

PowerPlot(power_array,
          par_to_search = 'sd',
          find_lowest = FALSE,
          slicer = list(n = 30))

## Adding an example works the same: If we expect a delta of 1, and the n =
## 30, what is the maximal SD we can have still yielding 90% power?

AddExample(power_array,
           find_lowest = FALSE,
           slicer = list(n = 30),
           example = list(delta = 1),
           target_value = .9)